반응형
Notice
Recent Posts
Recent Comments
Link
- Today
- Total
02-13 08:43
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- HTTP
- Python
- 딥러닝
- rxswift
- 오블완
- swiftUI
- Observable
- substr
- rest api
- MVC
- Request
- deeplearning
- SWIFT
- Optional
- decode
- tapply
- scheduledTimer
- ios
- cocoapods
- barplot
- 티스토리챌린지
- 연산자
- struct
- sigmoid
- 명령어
- 시각화
- r
- Linux
- ReLU
- SQL
Archives
iOS 개발 기록 블로그
딥러닝의 시그모이드(sigmoid), 렐루(Relu), 행렬의 내적 본문
반응형
시그모이드 함수
시그모이드 함수의 식이 왜 아래와 같을까
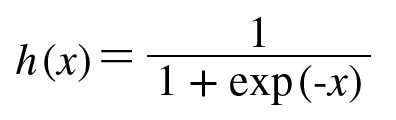
통계학에서 성공할 확률이 실패할 확률보다 얼마나 큰지를 나타내는 오즈비율이라는 값이 있다.
오즈 비율 = (성공 확률) / (실패 확률)
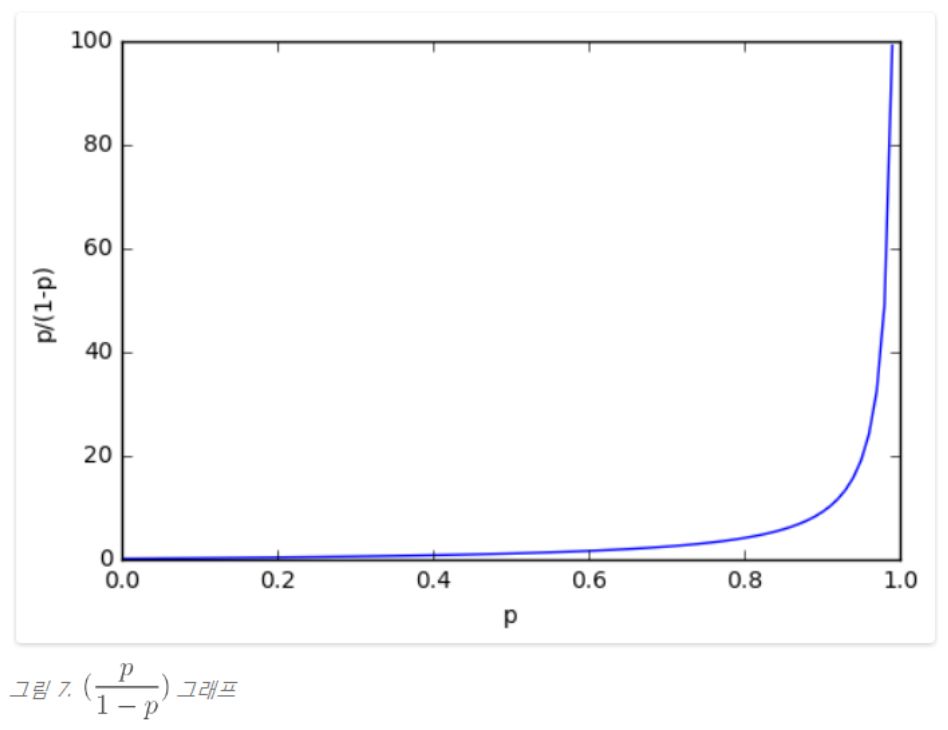
성공할 확률 P를 0~1 사이의 값으로 나타내면 실패할 확률은 1-P이다
위의 그래프에서 P(성공할 확률) 가 1에 가까우면 오즈비율 (성공할 확률이 실패할 확률보다 얼마나 큰지) 값이 급격히 커져버리는 현상이 발생한다.
급격히 커져버리는 현상을 방지하기 위해서 이 함수에 로그를 취한게 logit 함수이다.
그래프는 아래와 같다

P가 0.5 일 때 실패할 확률 대비 성공할 확률이 0이 된다
P = 0.5 일 때는, 0이 되고
P = 1 일 때는, 무한히 큰 양수,
P = 0 일 때는, 무한히 큰 음수를 가지는 특징이 있다.



렐루 함수 (Relu)
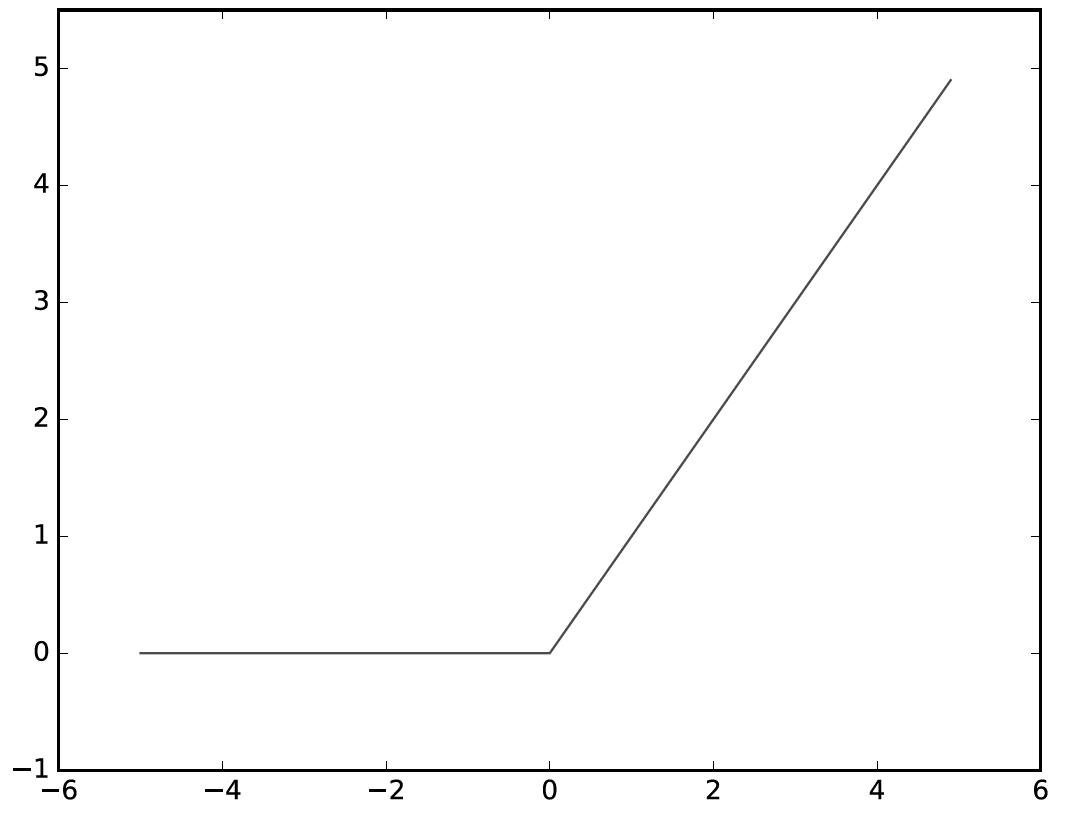
Relu 는 입력이 0을 넘으면 그 입력을 그대로 출력하고 0 이하면 0을 출력하는 함수
예제) Relu 함수를 파이썬으로 구현하시오

numpy version)

예제) Relu 함수를 시각화하시오

다차원 배열의 계산
넘파이로 행렬을 만들고 차원 수 확인과 몇 행 몇 열인지 확인하는 방법

행렬의 내적

예제) 행렬의 내적을 numpy로 구현하시오


반응형
'Deep Learning' 카테고리의 다른 글
| 딥러닝 소프트맥스(softmax) 함수 공식 구현 과정 (0) | 2022.01.05 |
|---|---|
| 딥러닝 신경망의 내적, 3층 신경망 전체 코드 (0) | 2021.12.23 |
| 신경망 함수 종류와 시각화 (step func, sigmoid func) (0) | 2021.12.04 |
| 딥러닝 파이썬으로 퍼셉트론 AND, OR, NAND, XOR 게이트 구현하기 (0) | 2021.12.03 |
| 머신러닝의 종류와 퍼셉트론(Perceptron)의 역사와 예 (0) | 2021.11.29 |




